Runtime warnings, errors, and debugging in R and Stan

FW 891
Click here to view presentation online

Christopher Cahill

13 September 2023

Purpose

  • Talk through some common errors and warning messages in Stan
  • Most of this is available on the Stan webpage
    • Can be useful for debugging or improving models
  • How I debug Stan files (probably the only way)
  • How I debug R code (not the only way)

Runtime warnings and convergence problems webpage and cmdstan documentation:


https://mc-stan.org/misc/warnings.html


https://mc-stan.org/docs/2_24/cmdstan-guide-2_24.pdf

Overview

  • Stan throws a range of diagnostics, and throws warnings or errors for anything suspicious
  • Some of these are more important than others, but in general having an understanding of these warnings and errors can help you debug models or figure out problems with your model
  • Figuring out what’s going on is as much an art as science

The folk theorem of statistical computing

  • This is a pithy rule that originated from Andrew Gelman (author of Bayesian Data Analysis). It is paraphrased as


“When you have computational problems, often there is a problem with your model [rather than the software]”—— Andrew Gelman

Types of warnings

  • Divergent transitions after warmup
  • Exceptions thrown when Hamiltonian proposal rejected
  • R-hat
  • Bulk and Tail ESS
  • Maximum treedepth
  • BFMI low

Divergent transitions after warmup

  • Probably the most important warning
  • Commonplace with mixed effects models
  • Hamiltonian Monte Carlo provides internal checks on efficiency and accuracy
    • These come free, arising from constraints of the physics simulation
  • Recall that HMC simulates a frictionless particle
    • In any given transition, total energy at the start of a simulation should be equal to the total energy at the end
    • When this doesn’t happen, the energy is “divergent”
      • often means the posterior distribution is very steep in some region of parameter space, hard to sample

McElreath 2023

Divergent transitions after warmup

  • Critical to recognize that divergent transitions cannot be safely ignored if completely reliable inference is desired
    • Proceed at your own risk: you may not be faithfully representing the posterior uncertainty if you ignore DTs
  • If you only get a few divergences and good Rhat values and ESS, the resulting posterior is often good enough to move forward
  • There are cases where a small number of divergences without any pattern in their locations can be shown to be unimportant, but this requires a lot of simulation and math
  • The bottom line is your inferences may be biased if there are DTs after warmup

Diagnosing and eliminating divergences

Divergent transitions after warmup

How to deal with DTs:

  1. Double check the code (even coding errors can cause DTs)
  2. Increase the adaptation target acceptance statistic, adapt_delta, > 0.8
    • Must be between 0,1, so values >> 0.999 have diminishing returns
    • The step size used by the numerical integrator underlying Stan is a function of adapt_delta, so this results in a smaller step size and (sometimes) fewer divergences
  3. If (2) does not work, consider priors or reparameterizing the model
    • Plot the data, hone in on where in the model the divergent transitions are occurring
    • Lots of pairs plots, divergent transition plots
    • DTs can indicate many things, and often reveal information about your experimental design or the lack of information content contained in your data
  4. Weep 😭

https://mc-stan.org/misc/warnings.html

Exceptions thrown when Hamiltonian proposal rejected

Exception thrown at line 24: normal_log: Scale parameter is 0, 
but must be positive! 
-----
Rejecting initial value:
Gradient evaluated at the initial value is not finite.
Stan can’t start sampling from this initial value.`

  • First warning indicates that the standard deviation parameter of the normal distribution is zero, but it must be positive for Stan to compute the density function

  • The second message indicates that the gradient of the target (as computed by Stan’s automatic differention) is infinite, indicating numerical problems somewhere in the model but unfortunately without clear information about where exactly.

Exceptions thrown when Hamiltonian proposal rejected

Exception thrown at line 24: normal_log: Scale parameter is 0, 
but must be positive! 
-----
Rejecting initial value:
Gradient evaluated at the initial value is not finite.
Stan can’t start sampling from this initial value.`
  • Note: it is possible that even in a correctly specified model a numerical inaccuracy is occasionally seen, especially during warmup
    • For example, scale parameter with zero lower bound can still become numerically indistinguishable from zero

https://mc-stan.org/misc/warnings.html

Split-\(\widehat{R}\) aka Rhat

  • This statistic compares means and variances of the chains
  • Remember, we use several chains to make convergence diagnostics easier, starting chains at different starting points
  • Values < 1.1 often sufficient
    • We remove draws from the beginning of the chains and run the chains long enough so that it is not possible to distinguish where each chain started
    • A fair amount of math behind this (see link below)

https://avehtari.github.io/masterclass/slides_rhat_neff.pdf

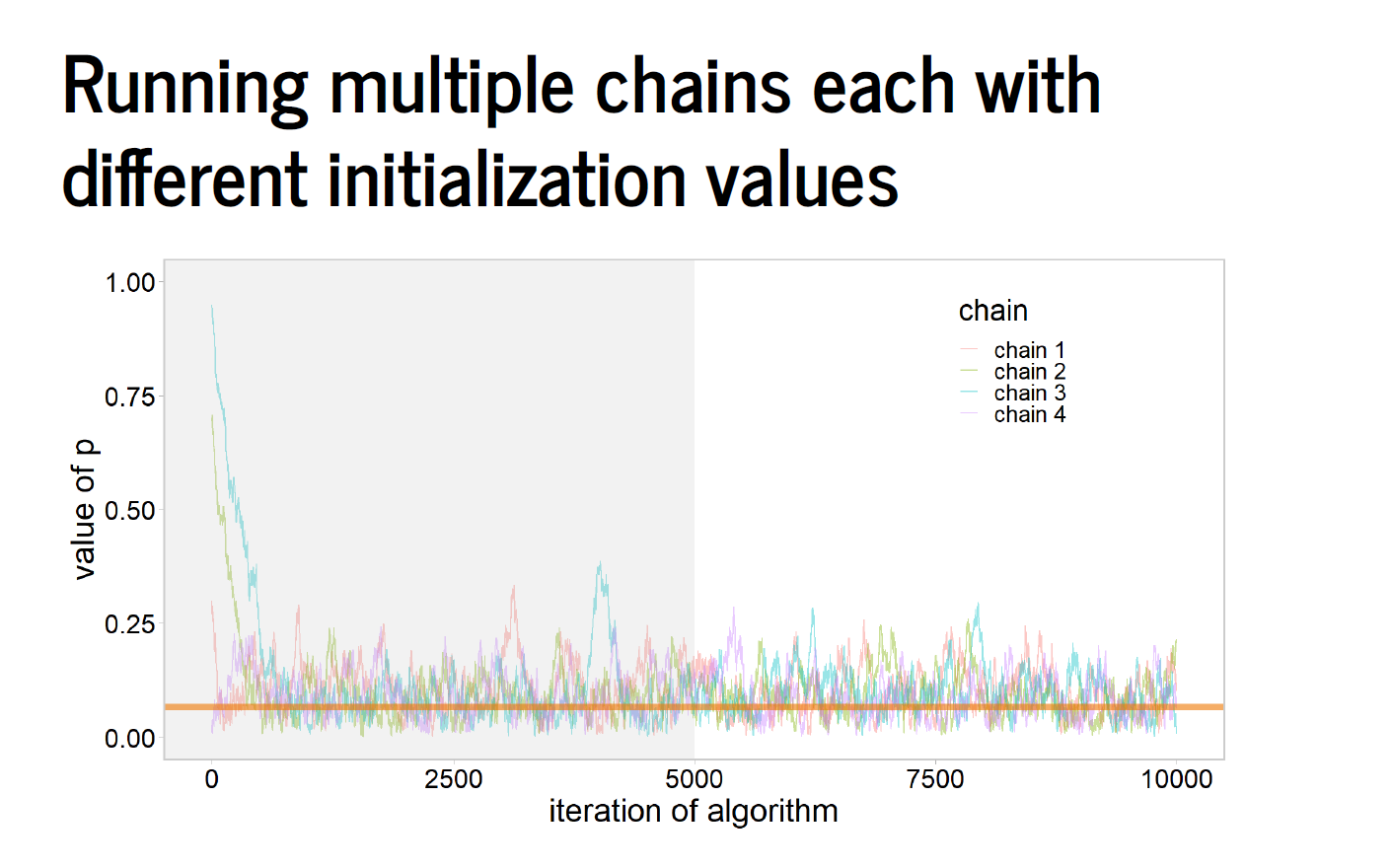
Some slides from Aki Vehtari on convergence to a common posterior

See here:

https://avehtari.github.io/masterclass/slides_rhat_neff.pdf

Nonconvergence

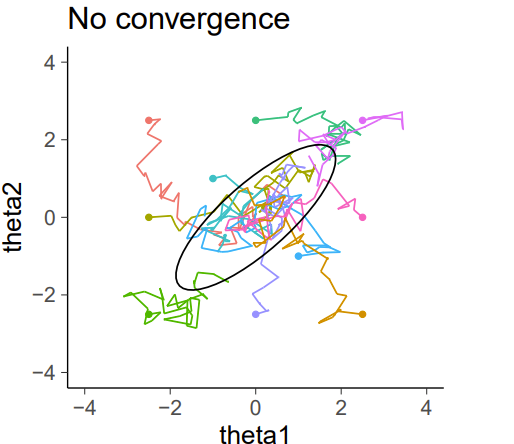
https://avehtari.github.io/masterclass/slides_rhat_neff.pdf

Nonconvergence viewed another way

https://avehtari.github.io/masterclass/slides_rhat_neff.pdf

Visually converged chains

https://avehtari.github.io/masterclass/slides_rhat_neff.pdf

High \(\widehat{R}\) values

  • Indicate the chains have not mixed well
  • Good reasons to NOT think of them as being fully representative of the posterior = bad inference
  • When there are also DTs in the model, just another symptom of problematic geometry that caused the divergences
  • If high \(\widehat{R}\) without other warnings, often associated with posteriors that have multiple, well-separated modes
  • Running chains longer may help

https://mc-stan.org/misc/warnings.html; Gelman et al. 2003

Bulk and tail Effective Sample Size (ESS)

  • Roughly speaking, ESS tells you how many independent draws contain the same amount of information as the dependent sample obtained by the MCMC algorithm
  • Higher is better
  • For final analyses, Stan recommends bulk-ESS > 100x the number of chains
    • 4 chains, want rank-normalized ESS of at least 400
    • Early in an analysis, ESS > 20 is fine

https://mc-stan.org/misc/warnings.html

Bulk and tail Effective Sample Size (ESS)

  • Tail-ESS computes the minimum of the ESS of the 5th and 95th quantiles
    • Warnings about tail-ESS can help diagnose slow mixing in the tails
  • These warnings are often accompanied by large \(\widehat{R}\) values
  • Useful quick summary, but for final results it can be useful to check Monte Carlo standard error for quantities of interest (not shown)
  • Introduce thinning, and the only reason to do it

https://mc-stan.org/docs/reference-manual/effective-sample-size.html

Maximum treedepth warnings

  • Not as serious as other warnings
    • DTs, high \(\widehat{R}\) and low ESS are a validity concern
    • Maximum treedepth warnings are an efficiency concern
  • Configuring the NUTS sampler (variant of HMC used by Stan) involves putting a cap on the number of simulation steps it evaluates during each iteration
    • This is controlled by the max_treedepth parameter, where maximum number of steps = 2^max_treedepth
  • If you are only getting this warning and other diagnostics are good, likely safe to ignore (but you may lose out on efficiency)

<https://mc-stan.org/misc/warnings.html#bulk-and-tail-ess >

Bayesian Fraction of Missing Information (BFMI)

Example:

The E-BFMI 0.2786 is below the nominal threshold of 0.3 
which suggests that HMC may have trouble exploring the target 
distribution.
  • There is an energy__ output from Stan’s samplers is used to diagnose the accuracy of HMC
  • Implication of this warning is that HMC is not exploring the posterior well, in particular the tails of the posterior
    • Run the model longer or reparameterize your model
  • Mathematically dense (see Betancourt 2016) https://arxiv.org/pdf/1604.00695.pdf

Debugging Stan code

  • Stan provides print() statements that can print literal strings and the values of expressions
  • print(): accepts any number of arguments
for (n in 1:N) { 
    print("loop iteration: ", n); ... 
}
  • Each time the loop body is executed, it will print the string “loop iteration:” (with the trailing space), followed by the value of the expression n, followed by a new line

https://mc-stan.org/docs/reference-manual/print-statements.html

Useful things to do with print()

  • Very useful for debugging, particularly when coupled with target()
    • target() is the log density accumulator, and is actually a reserved word in Stan
vector[2] y;
y[1] = 1;
print("log density before =", target());
y ~ normal(0,1);  // bug!  y[2] not defined
print("log density after =", target());

https://mc-stan.org/docs/reference-manual/print-statements.html

Debugging R code

  • Ten minute warp-speed lesson on debugging in R
  • Several ways to do this, but here we’ll do a demo of the functions traceback() and browser()

traceback()

foo <- function(x) { print(1); bar(2) }
bar <- function(x) { x + a.variable.which.does.not.exist }
# foo(2) # gives a strange error
# Error in bar(2) : object 'a.variable.which.does.not.exist' not found
traceback()
2: bar(2) at #1
1: foo(2)
  • identifies which function generated the error

browser()

  • Abstract and not well implemented (Belinsky, pers comm 2023)
  • This is what I (Cahill) mainly use to debug R code
  • Interrupts the execution of an expression and allow the inspection of the environment where browser was called from
my_fx <- function(x){
    y <- x^2
    z <- y - x + 3
    a <- z - 1 / y
    a
}

my_fx(1)
[1] 2

browser()

# demonstrate some weird behavior:
my_fx(NA)
[1] NA
my_fx(3)
[1] 8.888889
my_fx(0)
[1] -Inf
  • Put a browser() in it to win it

https://stat.ethz.ch/R-manual/R-devel/library/base/html/browser.html

browser()

my_fx <- function(x){
    browser() # slap a browser in it
    y <- x^2
    z <- y - x + 3
    a <- z - 1 / y
    a
}

my_fx(0) # call the function
  • Go to R to demonstrate how to use
  • Note this works with for-loops and other horrid things

Summary and outlook

  • Went through some common Stan runtime warnings and error messages
    • Discussed that some checks are about the validity of inferences while others are about efficiency
  • Debugging Stan code via print() statements
  • Debugging R code via traceback() and browser()
  • Next few weeks, move into nonlinear and mixed effects modeling (where we will experience some of these warnings/issues)

References

Betancourt, M. 2016. Diagnosing suboptimal cotangent disintegrations in Hamiltonian Monte Carlo. https://arxiv.org/pdf/1604.00695.pdf

Gelman et al. 2003. Bayesian Data Analysis.

McElreath 2023. Statistical Rethinking. Second Edition.

Stan documentation. 2023. https://mc-stan.org/docs/reference-manual/index.html